平均算という個別単元を見かけた。

平均を求めたり、平均に関連した算数の問題は目にしているけど、「平均算」という単元として取り扱われていることは、少し新鮮な感じがする。

平均の基本的な公式は、『個々の数を全て足して、個数で割る』。

例えばこんな例題。

『はるなちゃん、なつき君とあきと君のテスト結果は、それぞれ80点、60点、100点でした。3人の平均点をもとめなさい。』

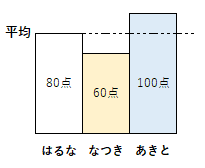
（80点 + 60点 + 100点) ÷ 3人 = 80 答え 80点。

逆に平均点が分かっていて、そこから個の点数を導き出す問題は、下記のような例題。

『はるなちゃん、なつき君とあきと君の３人で町内会の射的ゲームに出場しました。３人一組で平均80点以上だと次のステージに進むことができます。最初にはるなちゃんが80点を取り、次になつき君が60点を取りました。最後のあきと君が何点を取れば、次のステージに進むことができるでしょうか。』

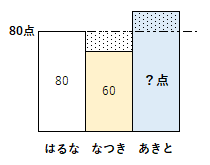
公式を使って解くと、平均80点 x 3人 = 合計240点　　240点 – 80点 – 60点 = 100点　 答え　100点。

現実的な場面での考え方でいくと、最初にはるなちゃんがステージを突破するための個人ノルマ80点を取った。続いて、なつき君は60点しか取れなかった。最後のあきと君は個人ノルマ80点に加えて、なつき君がノルマに足りなかった20点分を補わなくてはならない。

この場合は、個人ノルマ（平均点）の80点 + (80点 – 60点) = 100点　　答え　100点。　

平均算では、『平均を上回っている部分　と　平均を下回っている部分　の面積は等しい。』という理解も必要。

だって『平均』なんだから。

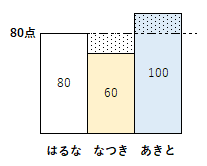
言い換えると、平均算は『凸凹をならして、そろえる』イメージ。上図の青ドット部分と白ドット部分は等しい。

例題は３名だけど、個数が増えたとしても、考え方は同じ。

『ふゆひこ君は5教科のテストを受け、平均点は82点でした。国語96点、算数100点、理科86点、社会84点だったとき、タイ語は何点だったでしょうか。』

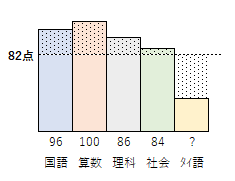
公式に当てはめると以下の通り。

『凸凹をならして、そろえる』やり方でも答えを導き出せる。

応用問題になっても、考え方は変わらない。以下のような応用問題でも同じ様に解くことが出来る。

『ある学年の生徒数は６０人で、平均身長は144cmです。男子生徒だけの平均身長は141.8cm、女子生徒だけの平均身長は145.8cmでした。この学年の女子生徒の人数は何人ですか。』

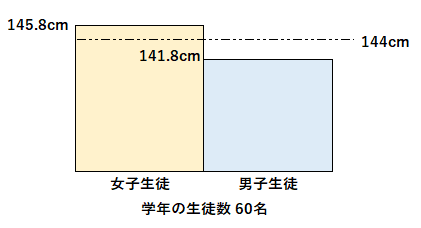
問題を解くにあたって、図を書いて表現することが大切。問題の内容を図に正しく落とし込むことが出来ると、すでに半分は解けたようなもの。

女子も男子も生徒数がわからないので、公式ではなく『凸凹をならして、そろえる』で解いてみる。

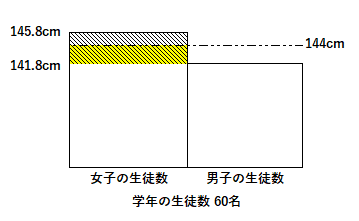
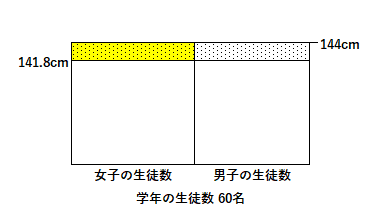
『平均を上回っている部分と、平均を下回っている部分の面積は等しい。』

今回は少し変則的に凸凹に加えて、141.8cmのライン以上で考える。『左図の斜線部分と、右図のドット部分の面積は等しい。』

左図の斜線部分　(145.8cm – 141.8cm) x 女子の生徒数 = 4cm x 女子の生徒数

右図のドット部分　(学年平均144cm – 男子の平均141.8cm) x 60名 = 2.2cm x 60名 = 132cm

4cm x 女子の生徒数 = 132cm となる。よって　女子の生徒数は、132cm ÷ 4cm = 33名。　　

この問題は、比を使っても解くことも出来る。

まず　女子生徒の平均身長、学年の平均身長、男子生徒の平均身長の差に注目する。

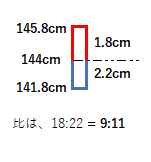
『凸凹をならして、そろえる』、つまり、『平均を上回っている部分と平均を下回っている部分の面積は等しい』ことより、タテの比が9:11ならば、ヨコの比は11:9になる。

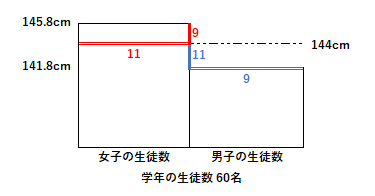
生徒数の比は、女子：男子＝１１：９、合計数が６０名だから、女子の生徒数は　60 x 11/20 = 33名。

『比と割合』を使いこなせるようになると、『ＯＸ算』の多くに有効活用できます。